Sunday, April 29, 2007
HARD HOMEWORK!!
Thursday, April 26, 2007
What happened on April 26th
 Mutually exclusive and inclusive events only apply to probability.
Mutually exclusive and inclusive events only apply to probability.Mutually exclusive events are two events that cannot happen at the same time. An example of this would be the probability of being male or female. You cannot be male-female, or female-male.
Mutually inclusive events are two events that can happen at the same time. An example of this would be the probability of drawing a red and the probability of drawing a jack in a deck of cards. It is possible to draw a red jack.

 In that case, when you are calculating the probability of drawing a jack or a red, you must remember that there are two red jacks. This means that you cannot count the red jacks twice, so you must minus 2/52. Below is a link to a spreadsheet that Mr.Max created that may help you understand this concept better
In that case, when you are calculating the probability of drawing a jack or a red, you must remember that there are two red jacks. This means that you cannot count the red jacks twice, so you must minus 2/52. Below is a link to a spreadsheet that Mr.Max created that may help you understand this concept better
 Above is the formula for when events are mutually exclusive.
Above is the formula for when events are mutually exclusive.
Below is the formula for when events are mutually inclusive.
Due for April 26th are questions 1,3,5,7, and 9 out of a booklet that we were handed out yesterday.

Tuesday, April 24, 2007
Tuesday April 24th
Today we started off with mental math of course:).
If you were absent from class, or just forgot, we have a Probability Test on Tuesday May 1st, our review is on Mon the 30th, and accelerated math is due Monday April 30th as well. We are to have completed 22 objectives. The wiki assignment is due on Friday May 4th at the end of the day.
Mr. Max went over what you should have gotten for the answers to Question 3 Part B in the Design and Measurement Portfolio. His answers were; $8932.00 for Method #1, and the total for Method #2 was $11,541.75 he also informed us that he purchased the material in whole cubic yard units, which is pretty important.
Don't forget that we are to finish question's 3&4 in the Personal Finance Review, but I am not positive when the exact due date was for them.
Monday, April 23, 2007
Friday, April 20, 2007
Free Marks For a Homework Check
1. What did you do this week without your teacher? (i.e. How much of the assigned work have you completed?)
2. What have you got left for homework?
Have a great weekend, folks...
RM
Thursday, April 19, 2007
Max's Absence - Day 2
1. Witness your thoughts. No one can stop thinking entirely; it is impossible. If you start trying not to think, you only end up thinking about how to stop thinking! What you can do, however, is to withdraw from your thoughts and become more of an objective spectator.
2. Picture your mind as a blank canvas or a dark sky. Allow your thoughts to come and go, but resist the urge to follow each one. Your brain will eventually slow down and you will feel less pressured.
3. Count. If you find it difficult to let go of your thoughts, try counting slowly as you breathe. Watch your thoughts and try to resist following them. Turn your attention to the count as you breathe out.
4. Pay active attention. As you work and think, try to keep your attention on the task at hand, Be strict with yourself, and each time your mind wanders, return it to the task. As you keep refocusing your attention, your “mind stillness” will improve.
5. Still your body. One sign of fragmented attention is fragmented movement. For example, when you are at the theatre, it is easy to tell if others around you are fully attentive to the performance. People who sniff and sigh, move their heads this away and that, and wiggle in their seats are having some difficulty concentrating. Rapt attention is usually accompanied by still body posture.
6. Find a comfortable position and don’t allow yourself to move. Concentrate on what you are doing or watching, drawing your attention away from physical distractions, and focus your thoughts on your task. After a while, you will notice that you fidget less and feel less physical discomfort. You are now channeled into mental exertion.
7. Interest your mind. Try to find interest in projects to help you concentrate. Taking up a new hobby can be a tremendous help. You should also try to find something interesting even in the dullest chore. If you are at a gathering, find someone and start a conversation. Be inquisitive and you might discover you have similar interests.
8. Open the mind. Just as strength, stamina, and flexibility must be incorporated in your physical routine, the mind needs new and absorbing challenges to give it a change from its everyday journey. Notice something new on the same way home that you might not have noticed before. Buy a magazine on a subject you normally wouldn’t look at, read it, and open yourself to new possibilities.
Wednesday, April 18, 2007
Day One Max's Absence
1. Accelerated Math
- The probability objectives are due at the end of the unit (upon Max,s return). We are also responsible to print other practises, exercises, and tests.
- If help is needed turn to your peers or feel free to email Max with any serious questions.
2. Wiki Assignment
- There are instructions posted on a prior blog from Max and 'bend' included a link to view older assignments.
- Remember having your laptop is a privilege and if you don't correctly use them will have it taken away. You will need it to finish some assignments so keep this in mind.
3. Design & Measurement Package
- You should come familiar with this package as the first section of the exam will be on this section.
- Do Question #6 Question B (Driveway)
4. Personal Finance Questions
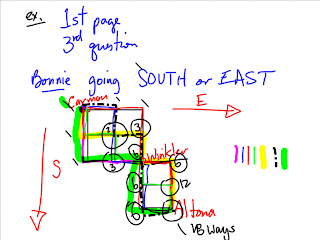
- #3(Maila) & #4(Bonnie)
- We took notes on this section before spring break and you are also encouraged to view the network or blog for help.
Well that's our list of things to do for the next couple days, so make sure you properly use the time your given to get it all finished in time.
Also on the blackboards in the classroom rules have been listed for the classroom that will apply while he is absent and his email addresses will also be found there to contact him for help.
BlOnDiEb
Monday, April 16, 2007
Work, Work, Work
The class started off with him explaining to us all of the expectations and how we were to act for the sub, like not to be playing games on your computers and such. Once that spiel was done he explained what a 'Wiki' was and how it was used. So all of you out there who struggle with some of the Accelerated Math objectives never fear! Hopefully the Wiki's will help you out. I encourage all of you to add to our Wiki as often as possible.
Click here to see some of last semester's Wikis and how they did them
Mr. Max explained to us that apparently the letters 'pb' in the address meant that making a Wiki was as easy as making a peanut butter sandwich, and Ryan was kind enough to point out to all of you that I am allergic to peanuts!
Then he gave us a bunch more problems for us to work on in his absence. They are as follows....
ACCELERATED MATH UP TO OBJECTIVE 20ish. (PROBABILITY)
DESIGN AND MEASUREMENT BOOKLET PG.6 B.
HINT!! -> CONSIDER USING A SCALE DIAGRAM
-> CONSIDER USING EXCEL
PERSONAL FINANCE BOOKLET #3 and #4
**USE EITHER EXCEL OR TVM SOLVER**
Finally he got us to give him our e-mail’s once again so we were able to register for Wiki.
What To Do With Your Wiki
1. Your assignment goes on www.appliedmath.wikispaces.com. If you've given me a valid email address, you should be an authorized contributor.
2. You're essentially teaching someone how to do a 'type-problem' from Accelerated Math, from start to finish. Show the entire problem, the objective, any relevant instructional materials, whatever....and I believe that I said in class that it should be something you struggled with yourself, but that you're competent with now.
3. Remember that once a question/objective has been selected, it's not available for anyone else's assignment. Check carefully before you post.
4. It's a wiki, so SAVE YOUR CHANGES every time you make some....works in progress are fine, but I'll check regularly to make sure you have something up.
5. No last names/identifiers in your posts...We've talked about this in class...please remember to be 'mostly anonymous'....
Have fun, be experimental, and try to learn something on purpose....
RM
Math is awesome
Well we started out the class with watching a very powerful short film on a family in the east that received a great gift from some people in the States. It makes me sad to watch little films on what's going on in the World but it also makes me think on what I can do to help.
After we watched that film, Mr. Max decided to do a homework check on the homework that was assigned yesterday.
We shortly after, corrected the assignment in class. So for those who didn't get it done be sure to do that soon.
Homework assignment: Probably Review Booklet: #5, 11, 14,15,16, 18, 19
Thursday, April 12, 2007
"brio" - Enthusiastic vigor; vivacity; liveliness; spirit.
I had seen the presentation already this morning but I knew that the probability of me actually doing any work this block was less than 1/8th so I went to the presentation again.
The presentation was about world hunger and the war in northern Uganda, in the presentation we were told things like:
- Every 3 seconds a child dies due to extreme poverty
- 800 million people go to bed hungry each night
- 1.2 billion people live on less than $ 1.00 per day
- $ 13 million could help to serve the basic needs of impoverished people across the globe (that's less than is spent on pet food yearly)
- It has been proposed that world hunger could be cut in half by 2015, but hunger rates are increasing
- The Canadian Food Grains Bank, now "End Hunger", dates back almost 500 years
- The Canada Government matches all money raised towards ending world hunger at a 4:1 ratio with a
$ 16 million limit, soon to be raised to a $ 20 million limit - 50 % of the world gets its livelihood from agriculture
- The population of Uganda is 28,816,000 Million people who speak 43 different languages
- 90 % of food consumed in northern Uganda is provided by humanitarian organizations
- The total Gross Domestic Product income is $ 45.97 billion yearly
- Polygamy is a common practice
- English is the official language but 62 % of people do not speak or write it
As well as many other interesting facts about Uganda and World Hunger. At the end of the presentation we were given the opportunity to ask questions and view pamphlets. We were also given other resources to look at:
http://www.micahchallenge.org/
http://www.foodgrainsbank.ca/
http://www.makepovertyhistory.ca/
Questions For Friday
Do numbers: 15, 16, 18, and 19...
The Fundamental Counting Principle as well as what we've covered already on Perms/Coms should help a lot.
RM
Wednesday, April 11, 2007
Permutations and Combinations April 11th






Tuesday, April 10, 2007
Editing or Growing Posts - April 10th
For the beginning of the class today, Mr. Max shared with us that Vicki A. Davis had left a comment on our blog. She has been known by many people across the web for the blogs she has published. She has taken the time to not only view but leave her opinion on how we're doing. Her comment was positive and she was impressed with our work. Good job class!! Although there were a few things that we can do to "Edit & Grow" our blogs to make them better for our classmates.
1. Pay Attention to comments.
-Answer questions when posted
-Clarify previous posts, or discuss with real people in real times
2.Don't use slang words, or colloquialisms.
-The local language needs to be improved
-Fix these problems
3.Correct A.S.A.P
-Spelling
-Punctuation
-Grammar
4. Stop Apologizing,
-Keep in mind that you are contributing to the class!
5.Avoid Plagiarism
-When you make a post it is assumed that the voice used is that of your own(if not provide documentation & references)
6.Make Tags for all of your contributions.
-Shown at the bottom of the "edit post" window
For the remainder of the class we were given time to work on our Permutaions and Combinations Assignments. Also Mr. Max printed out exercises in accelerated math for everyone so that we can begin to set due dates.
BlOnDiEb
Factorials
In Objective 14, you learn about factorials.
(when you see something like 5! + 4!)
I'll do an easy one,
if you see 4! that means that you take all the positive intergers less than or equal to 4, and multiply them. This gives you a result of 4*3*2*1=24
 There is a special case when you have 0! though. 0! is defined to have a value of 1.
There is a special case when you have 0! though. 0! is defined to have a value of 1. Ok, now that I got that down, I'll do a practice question.
6!+4! (a) 744 (b)1488 (c)17 280 (d)34 560
To start off, 6! is 6*5*4*3*2*1, which is 720,
and 4! is 4*3*2*1, which is 24
and 720+24 is of course 744
Therefore the answer is (a) 744
Hope that helped,
Aaron
Combinations
We can also use pascals triangle to figure out combinations, the triangle has infinite amount of rows and can go on forever. If, for instance, we are trying to find 10_C_4, we would take the fourth entry in the tenth row which would come out to 210, so this means that there are 210 ways to choose 4 numbers out of a set of 10 numbers.

This can be done from either side and you should get the same answer.
Combinations

n= total
r = want
! = factorial
Another way to find the nuber of combinations possible is as follows:
 By using the fundamental counting principle, there are 5 x 4 ways to choose the cards in order. The number of ways in which 2 cards can be arranged is 2! = 2 x 1. Therefore, the number of pairs of cards that can be chosen is:
By using the fundamental counting principle, there are 5 x 4 ways to choose the cards in order. The number of ways in which 2 cards can be arranged is 2! = 2 x 1. Therefore, the number of pairs of cards that can be chosen is:Permutations
Because order matters, we're finding the number of permutations of size 2 that can be taken from a set of size 3. This is often written 3_P_2. We can list them as:
CA CT AC AT TC TA
Now let's suppose we have 10 letters and want to make groupings of 4 letters. It's harder to list all those permutations. To find the number of four-letter permutations that we can make from 10 letters without repeated letters (10_P_4), we'd like to have a formula because there are 5040 such permutations and we don't want to write them all out!
For four-letter permutations, there are 10 possibilities for the first letter, 9 for the second, 8 for the third, and 7 for the last letter. We can find the total number of different four-letter permutations by multiplying 10 x 9 x 8 x 7 = 5040. This is part of a factorial.
To arrive at 10 x 9 x 8 x 7, we need to divide 10 factorial (10 because there are ten objects) by (10-4) factorial (subtracting from the total number of objects from which we're choosing the number of objects in each permutation). You can see below that we can divide the numerator by 6 x 5 x 4 x 3 x 2 x 1
Foot note
http://mathforum.org/dr.math/faq/faq.comb.perm.html
Combinations
I am here to talk to you today about combinations and give you all a fair bit of information that may help you to learn about combinations.
http://en.wikipedia.org/wiki/Combination - Wikipedia Website
http://mathforum.org/dr.math/faq/faq.comb.perm.html - Math Forum Wesbite
http://www.themathpage.com/aPreCalc/permutations-combinations.htm
This website has great information on both combinations AND permutations (helping out a little bit)
A combination is an un-ordered collection of elements.
The order of the elements within a combination is not important. For instance, the same elements within two lists are in different orders are still referred to as the same combination.
Also in combinations, elements are never to be repeated.
I hope this gives everyone a basic gist on what combinations are all about...
enjoy!
Permutations
Permutations...(from wikipedia) is the rearrangement of objects or symbols onto a distinguishable sequence. Each unique ordering is called a permutation. Permutations can have no repeats either. for example... ( see if I can make one up)
if you wanted to see all the ways you could take the letters from CARS, and make two letter "words", some permutations would be...
CA, CR, CS, AC, AR, AS, RC, RA, RS, SC, SA, SR,
( see that I never used CC, AA, RR, or SS )
there’s got to be more that can be taught about this and why it’s useful but this is all I have time for...
There is software for permutations, I didn't download it because I didn't have time and whatever but it's at this link.
These are other links that I used but didn't get all the info off of...you might want to use if you have any more questions that haven’t been answered
http://mathworld.wolfram.com/Permutation.html http://www.themathpage.com/aPreCalc/permutations-combinations.htm http://regentsprep.org/Regents/math/permut/Lperm.htm http://mathforum.org/dr.math/faq/faq.comb.perm.html
Monday, April 9, 2007
Permutations
Permutations are sometimes defined as any possible arrangement, or ordering, of the distinct items in a set. Or a way to arrange things in which order is important.
An example question:
If a softball league has 10 teams, how many different end of season rankings are possible? (Assume no ties)
Since we are ranking these teams that means the order is important. So we can use permutations to help us out.
We already know the formula is nPr from previous posts. So n is the number of teams we have to choose from. And we know from the information in the question that there are 10 teams.
So n=10.
R is the number of teams we are ranking at a time.
Again we know that r=10.
You put the numbers into the formula and you wind up with 10P10. After that you have to do the multiplication which is 10*9*8*7*6*5*4*3*2*1=3628800.
So this tells us that there are 3,628,800 ways to rank those 10 teams.
I hope my example question helped!
Marsha, Monday, April 9th
SO, I'm sure most everyone has started accelerated math and there are likely problems you will not understand. I took the liberty of surfing the old Math Wiki and tracked down some questions and explanations that I think should help.
A drawer contains 10 red socks, 4 white socks, and 8 blue socks. Without looking, you draw out a sock, return it, and draw out a second sock. What is the probability that the first sock is red and the second sock is white?
Answer
Two urns each contain green balls and yellow balls. Urn 1 contains four green bals and four yellow balls and urn two contains four green balls and three yellow balls. A ball is drawn from each urn what is the probability that both balls are yellow?
Answer
Two cards are drawn in succession from a deck of 52 playing cards. Find the probability that the king of clubs and any jack are drawn, in that order, without replacement.
Answer
Suppose that a license plate for a certain province consists of 5 distinct letters chosen form a distinct list of 8 letters followed by a 6 digit number where 0 is not the first digit which of the following expressions shows how many different license plates are possible? First figure out how many choices can be made for the letters or the numbers first your choice then find out the same for what’s left.
Answer
How many distinct arrangements can be made with the letters in the word SASKATCHEWAN? (is this correct?)
Answer
The Morse code is a system of dashes, dots, and spaces once used in Canada to send messages by telegraph. How many 7-character messages could be sent using 2 dashes and 5 dots?
Answer
There are 64 teams in a soccer tournament. Each team plays until it loses one game. There are no ties. How many games are played?
Answer
Firstly, Thanks Nemo for taking over my scribing duties as I was away. Today in class we did corrections, I'll make sure to post the slides as soon as I get back onto the laptops at school. For now bare with me as I complete the other part of the assigned math work and give you my explanation of permutations.
Google defines 'permuntation' as:
A reordering of that set where each element appears exactly once. For example, "egam" is a permutation of "game", or "2431" is a permutation of "1234".
I was searching through the old blog from last semester and found a post I had done a while back. Here's an example I had posted:
Jayla has two back pockets and one front pocket. She has 4 coins, how many ways can she put the coins in her pocket?
We figure this out by asking ourselves "how many ways can each coin be put in?" The answer is three seperate ways. Since Jayla had four coins we determine that the equation will be 3*3*3*3, which equals 81.
If you want to read the rest, click here.
Permutations
By the permutations of the letters abc it means all of their possible arrangements:
abc
acb
bac
bca
cab
cba
There are 6 permutations of three different things. As the number of things (letters) increases, their permutations grow astronomically. For example, if twelve different things are permuted, then the number of their permutations is 479,001,600.
Sometimes My Light Bulb Goes 'ON'....
At risk of gushing, I'm proud of how hard you guys as a class are trying to make these little brainwaves of mine work. This is an example of why we're blogging and why I truly believe that technologies such as our blog can make the whole greater than the sum of its parts.
Really neat stuff folks, and as your teacher, I'm glad to see you learn on purpose.
RM
Permutations and such...
anyways back to math....
Now i am sure this is going to be somewhat similar to what others have posted so please bare with me as i will try and find some new stuff on permutations!
A Permutation is the rearrangement of objects or symbols into distinguishable sequences. Each unique ordering is called a permutation.
as defined by the most helpful Wikipedia.
One person who played a major role in developing permutations was am man by the name of Augustin Louis Cauchy. He wrote a number of papers on the subject and this all happened around the year 1844.
Now the main formula for permutations is
---------> nPr <--------- n=is the number of digits you have to choose from
and
r=is the number of digits being used at a time (what you want)
....and if all of that mumbo jumbo didn't make sense to you, then here is an example which will hopefully help you out!
Question: >>>In how many ways can 8 CD’s be arranged on a shelf?<<<
Answer: First you must plug the numbers into the formula.
It would then look like 8P8.
After that you just have to do the multiplication which is 8*7*6*5*4*3*2*1= 40320
So there are 40320 ways to arrange that 8 CD's on the shelf. Wow that is a lot!
I am hoping that this scribe has helped you all understand permutations better. I know it helped me.
Permutations
Definition: A permutation is a set of objects that are arranged in a certain order, where the order is important.
Formula:

n is the total number of objects ; r is the number of objects chosen .
Examples:
You want to know how many orders your cd player will play your 13 song cd, on shuffle mode. At first there is a one in fourteen chance that any song will be played. The next song only has 1 in 12 chance of being played, because there are only 13 songs left to be played. The possibility of outcomes of a song being played decreases by one each time. The following will be the used formula.
P(n) = 13!
OR
P(n) = 13*12 * 11 * 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 =6227020800 ways of playing the same CD, in different orders.
Number 2 (from Webct learning)
How many five-letter "words" can be made from the alphabet if no letters are repeated? A "word" in this case is any five-letter arrangement with all letters different.
Solution:We will use the formula to answer this question.
The value of 'n' is 26 (there are 26 objects to choose from) and the value of 'r' is 5 (we pick five letters).

The formula may be convenient to use, but it is not essential. You can always find the number of arrangements (permutations) by multiplication as shown below.

Links
Permutations Calculator
Easy Permutations
More Examples
My Take On Permutations
A permutation is an arrangement of objects in different orders. The order of the arrangement is important!!
For example, the number of different ways 3 students can enter school can be shown as 3!, or 3·2·1, or 6. There are six different arrangements, or permutations, of the three students in which all three of them enter school.
The notation for a permutation: nPr
n is the total number of objects
r is the number of objects chosen (want)
(Note if n = r then nPr = n!)
Some examples of Permutations:
1. 5P5 = 5·4·3·2·1 = 120
2. 7P5 = 7·6·5·4·3 = 2520
Here are some Questions you may see and how you can figure out how to do them using the Permutations Formula (nPr) in use!!
1. What is the total number of possible 5-letter arrangements of the letters s,w,i,n,g if each letter is used only once in each arrangement?
5P5 = 5·4·3·2·1 = 120
( 5 letters to choose from, n#, want 5-letter arrangements, r#)
2. How many different 3-digit numerals can be made from the digits of 45678 if a digit can appear just once in a numeral?
5P3 = 5·4·3 = 60
( 5 numbers to choose from, n#, want 3-digit numerals, r#)
Also, as I was searching around I found some interesting websites on Perms & Cons that were helpful to me and thought I would share them with the rest of the class;
1. http://mathforum.org/dr.math/faq/faq.comb.perm.html ( This website gives the break down of how you start out on a question and take the information and put it into the formula)
2. http://regentsprep.org/regents/math/permut/PracPerm.htm (If your not to sure your doing this unit to right you can try these practice questions with the answers)
Permutations at thier finest
A single permutation of the letters ABC is BAC.
Consider the following question...
You were over at my house yesterday doing math homework. You accidentally forgot your binder and you need it now. But since I don't skip class I just tell you the password to my house's codelock. When you arrive at my house, you realize you forgot the combination. You remember the numbers, 8, 2, 1, 5, 6, but not the order they are supposed to be in. You are tempted to just start guessing random combinations. But how long would it take?
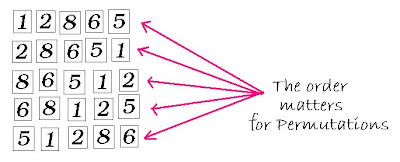
 So there are 120 ways to put the 5 numbers into my house's comboination lock.
So there are 120 ways to put the 5 numbers into my house's comboination lock. Combinations -Revised
ie: numbers, variables
the arrangement of elements into various groups without regard to their order in the group.
Many Common types of permutation and combination math problems, with detailed solutions
I'm not sure how useful it will be, I browsed through and it seemed to have potential, so hopefully it provides some useful information.
http://regentsprep.org/regents/math/math-topic.cfm?TopicCode=combin
Probability
We corrected Mr. Maxx’s mistake he made yesterday (the chance he used plane on all three legs of his journey). My answer was wrong, I knew once the fractions were up. The answer Mr Maxx got yesterday was 47/48; my answer was 31/48. The correct answer was 3/8. Maxx made a Tree diagram in Excel and saved it under the probability.
From the handout we were assigned questions to try. They are: #’s 9, 10, 22, and 27.
Tuesday, April 3, 2007
Is Homework a Waste of Time?
http://block3applied.blogspot.com/2007/04/test-day.html
I thought some people might like to see it so we could start up our own discussion about it...
Personally, I think that the amount of homework we are given in this class is reasonable and helpful. Its enough that you keep up with what we're doing but its not so much that you dread doing it.
Probability Cont.

He then asked us to come up with as many sample spaces for that example as we possibly could. Together we found these sample spaces:

We then concluded that sample spaces are a pain in the neck to create unless the total number of outcomes is fairly small. However it may be neccisary to create or verify a probability solution that has been calculated theoretically.
Fresh Start With Probability
 Next Mr. Max explained to us how Pascal's Triangle works. The two number above are added to together and this is continued throughout the triangle. For example: At the top of the triangle to get the answer "2" you add the two 1's above it. If your not to sure what I am talking about I will include the diagram that Mr.Max used to explain it to the class.
Next Mr. Max explained to us how Pascal's Triangle works. The two number above are added to together and this is continued throughout the triangle. For example: At the top of the triangle to get the answer "2" you add the two 1's above it. If your not to sure what I am talking about I will include the diagram that Mr.Max used to explain it to the class. Next thing we did was go over the things that we should recall or know from maybe Grade 11 ,and if you don't really remember very much don't worry you will catch on quick, but just remember to bring your calculator or as Mr.Max said that hundred thirty dollar thing sitting in front of you. You will be using it alot for Probability.
Next thing we did was go over the things that we should recall or know from maybe Grade 11 ,and if you don't really remember very much don't worry you will catch on quick, but just remember to bring your calculator or as Mr.Max said that hundred thirty dollar thing sitting in front of you. You will be using it alot for Probability. After we went over the general things and idea to help us understand what we will be doing in Probability, we were all handed out a Probability Review 2004/2005, where Mr.Max did Question #3 as an example to show us Pascal's Triangle in use.
After we went over the general things and idea to help us understand what we will be doing in Probability, we were all handed out a Probability Review 2004/2005, where Mr.Max did Question #3 as an example to show us Pascal's Triangle in use.